GNNs - 图神经网络学习笔记
参考AAAI 2020的Tutorial——Graph Neural Networks: Models and Applications以及一些资料来读论文,学习图神经网络领域知识。
GNNs - 图神经网络学习笔记
0 链接
Graph Neural Networks: Models and Applications, AAAI 2020 Tutorial
1 研究背景
相当多的数据是图/图谱(graph)结构的,如:
- 社交图谱;
- 传输图谱;
- 大脑图谱;
- 网页图谱;
- 分子图谱;
- 基因图谱。
一系列的实际问题都需要对图谱进行处理、特征提取和表征,例如:
- 链路预测;
- 节点分类;
- 社区检测;
- (网页)排序。
传统的深度学习方法所能处理的数据都是简单网格或序列,例如:
- 通过CNNs处理固定尺寸的图像/网格;
- 通过RNNs处理文本/序列。
然而图谱是由节点和边组成的,其形式是多变的:
- 各个节点的邻域节点数量各不相同;
- 图谱有着复杂的拓扑结构;
- 图谱也不存在固定的节点序列。
因此,图神经网络(Graph Neural Networks)被提出以解决这些问题。
2 理论基础
2.1 基本图论
Basic Graph Theory
2.1.1 图和图信号
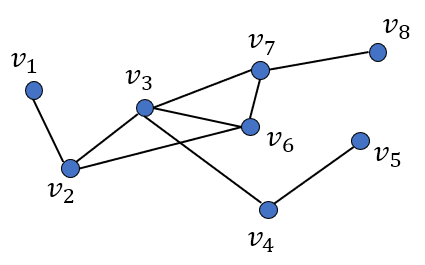
图
图(Graph)\(G\)由节点(Vertices)集合\(V\)和边(Edges)集合\(E\)组成,形式化为: \[ V = \{v_1, ... v_N\} \]
\[ E = \{e_1, ... e_M\} \]
\[ G = \{V, E\} \]
图信号
那么,图信号(Graph Signal)可形式化为映射\(f\): \[ f: V \to \mathbb{R}^N \]
或 \[ f: V \to \mathbb{R}^{N \times d} \] 即,映射\(f\)把每一个节点\(v\)映射为一个\(d\)维实数向量: \[ v \to [f(1), f(2), ... f(d)]^T \]
2.1.2 图的矩阵表示
度矩阵
度矩阵(Degree Matrix): \[ D = diag(degree(v_1), ... degree(v_N)) \] 在此例中: \[ D = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 4 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \]
邻接矩阵
邻接矩阵(Adjacency Matrix): \[ A[i,j] = \begin{cases} 1& v_i \in \mathcal{N}(v_j) \\ 0& v_i \notin \mathcal{N}(v_j) \end{cases} \] 在此例中:
\[ A = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix} \]
拉普拉斯矩阵
拉普拉斯矩阵(Laplacian Matrix): \[ L = D - A \] 在此例中:
\[ L = \begin{bmatrix} 1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 3 & -1 & 0 & 0 & -1 & 0 & 0 \\ 0 & -1 & 4 & -1 & 0 & -1 & -1 & 0 \\ 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 \\ 0 & -1 & -1 & 0 & -1 & 4 & -1 & 0 \\ 0 & 0 & -1 & 0 & 0 & -1 & 3 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 & -1 & 1 \\ \end{bmatrix} \]
2.2 谱图理论
Spectral Graph Theory
拉普拉斯矩阵可作为差分算子(difference operator),即: \[ h = Lf = (D - A)f = Df - Af \in \mathbb{R}^{N \times d} \]
\[ h(i) = \sum_{v_j \in \mathcal{N}(v_i)}(f(i) - f(j)) \in \mathbb{R}^d \]
可以理解为节点\(i\)与邻接节点的一阶距离之和。
拉普拉斯二次型(Laplacian quadratic form)可以表达图信号\(f\)的“平滑程度”(smoothness)或“频率”(frequency): \[ f^TLf = \frac{1}{2} \sum_{i,j=0}^{N-1} A[i,j] (f(i)-f(j))^2 \] > 公式推导可参考:谱聚类方法推导和对拉普拉斯矩阵的理解
可以理解为每对邻接节点之间信号的二阶距离。
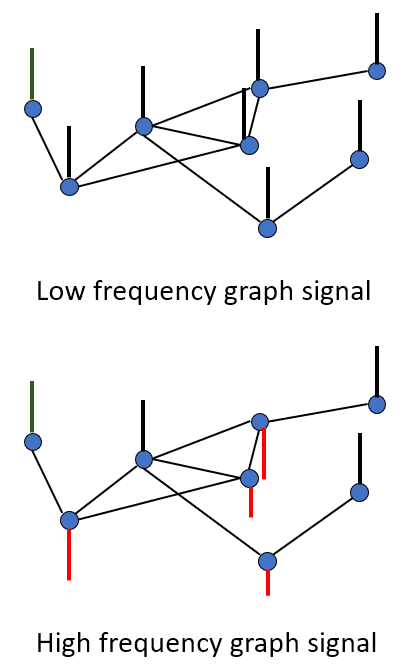
- 低频和高频图谱信号;
- 低频图信号中,每个图节点的信号接近,意味着图信号变化平缓,即周期长,在频域中低频多,高频少;
- 高频图信号中,每个图节点的信号相差较大,意味着图信号变化剧烈、频繁,即周期短,在频域中,高频多,低频少。
拉普拉斯矩阵是一个实对称半正定矩阵(a real symmetric positive semidefinite matrix),所以拉普拉斯矩阵满足:
- 一定有\(N\)个线性无关的特征向量;
- 特征值一定非负;
- 特征向量相互正交(特征向量组成的矩阵为正交矩阵)。
因为特征向量组成的矩阵为正交阵,所以满足:\(U^T = U^{-1}\)。因此,特征值与特征向量的公式\(L u_i = \lambda_i u_i\)的矩阵形式 \(L U = U \Lambda\)可以转换为: \(L=U \Lambda U^{-1} = U \Lambda U^T\),即拉普拉斯矩阵的特征分解。
通过拉普拉斯矩阵的特征分解(Eigen-decomposition of Laplacian Matrix),拉普拉斯矩阵具有一个完整的正交特征向量集合\(U \in \mathbb{R}^{N \times N}\)和特征值对角矩阵 \(\Lambda \in \mathbb{R}^{N \times N}\) : \[ L = U \Lambda U^T = \begin{bmatrix} u_0 & ... & u_{N-1} \end{bmatrix} \begin{bmatrix} \lambda_0 & & 0 \\ & \ddots \\ 0 & & \lambda_{N-1} \\ \end{bmatrix} \begin{bmatrix} u_0^T \\ \vdots \\ u_{N-1}^T \end{bmatrix} \]
拉普拉斯矩阵的\(N\)个非负实数特征值,满足非递减性质: \[ 0 = \lambda_0 < \lambda_1 \le ... \lambda_{N-1} \]
拉普拉斯矩阵特征分解的\(N\)个正交特征向量集合,即可作为该矩阵空间的正交基。每一个特征向量就代表一个基方向上的信号。把这个特征向量代入上述的计算信号频率的拉普拉斯二次型公式,正好可以推得特征向量的”频率“就是该特征向量对应的特征值: \[ f^T L f = u_i^T L u_i = u_i^T \lambda_i u_i = \lambda_i \]
因此,在该特征分解中,特征向量\(u_i \in \mathbb{R}^N\)对应的特征值\(\lambda_i\)被称为 \(u_i\) 的频率(frequency)。
2.3 图傅里叶分析
Graph Fourier Analysis
2.3.1 图信号的傅里叶分解
信号\(f \in \mathbb{R}^N\)可以通过图傅里叶级数(Fourier series)进行表示: \[ f = \sum_{i=0}^{N-1} \hat{f_i} \cdot u_i = \sum_{i=0}^{N-1} (u_i^T f) u_i \] 其中,\(u_i \in \mathbb{R}^N\)表示图傅里叶模式(Fourier mode),在图傅里叶变换中是图谱拉普拉斯矩阵的特征向量;\(\hat{f_i} \in \mathbb{R}\)表示图傅里叶系数(Fourier coefficient),通过图傅里叶变换取得。
图信号的傅里叶分解指的是用\(N\)个傅里叶模式向量,加权求和,表示图信号。
2.3.2 图傅里叶变换

图傅里叶变换(Graph Fourier Transform, GFT)指的是将图信号从空域(spatial domain)中的空域信号\(f\)变换到频域(spectral domain)中的频域信号\(\hat{f} \in \mathbb{R}^N\): \[ \hat{f} = U^T f = [u_0^Tf, u_1^Tf, ... u_{N-1}^Tf]^T \]
其中,\(\lambda_l \in \mathbb{R}\)表示频率,\(n\in[1, N]\)表示图节点。
频域信号\(\hat{f}\)实际上是傅里叶模式的权重,例如:\(\hat{f_i} \in \mathbb{R}\)是傅里叶模式\(u_i\)对应的权重,称为傅里叶系数。在此处的公式中,该傅里叶系数的计算原理实际上就是内积距离(相似度),即:\(\hat{f_i} = u_i^T f\),傅里叶系数 \(\hat{f_i}\)实际上是傅里叶模式\(u_i\)与空域信号\(f\)之间的相似度。
小结:图傅里叶变换将图信号\(f\)转换为了正交基\(U=[u_1, u_2, ... u_N]\)上的一组权重系数\(\hat{f}=[\hat{f_1}, \hat{f_2}, ... \hat{f_N}]\)。
2.3.3 逆图傅里叶变换
既然图信号\(f\)能够通过正交基上的一组权重系数进行表示,那么通过这组系数重新对正交基加权求和,显然可以逆变换回去,还原出空域的图信号\(f\)。
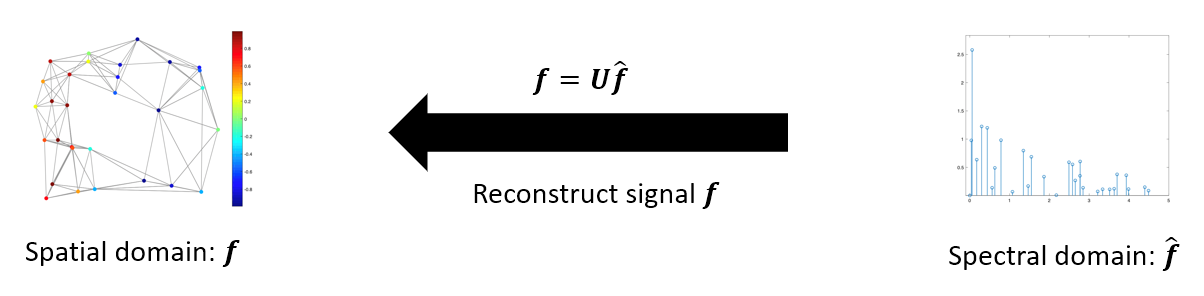
逆图傅里叶变换(Inverse Graph Fourier Transform, IGFT)指的是将图信号从频域\(\hat{f}\)变换回空域\(f\): \[ \begin{equation} \begin{split} f & = U\hat{f} \\ & = [u_0, u_1, ... u_{N-1}] \begin{bmatrix} \hat{f_0} \\ \hat{f_1} \\ \vdots \\ \hat{f_{N-1}} \end{bmatrix} \\ & = [u_0 \hat{f_0}, u_1 \hat{f_1}, ... u_{N-1} \hat{f_{N-1}}] \\ & = \sum_{i=0}^{N-1} u_i \hat{f_i} \end{split} \end{equation} \]
小结:逆图傅里叶变换以\(\hat{f}\)作为正交基\(U\)上的权重系数对正交基向量进行加权求和,变回了原始空域信号\(f\)。
3 模型
3.1 概述
图神经网络的目的在于解决图结构数据上的问题,而图结构数据的研究问题可分为两类:
- 节点级(Node-level):链路预测、节点分类等;
- 图谱级(Graph-level):图谱分类等。
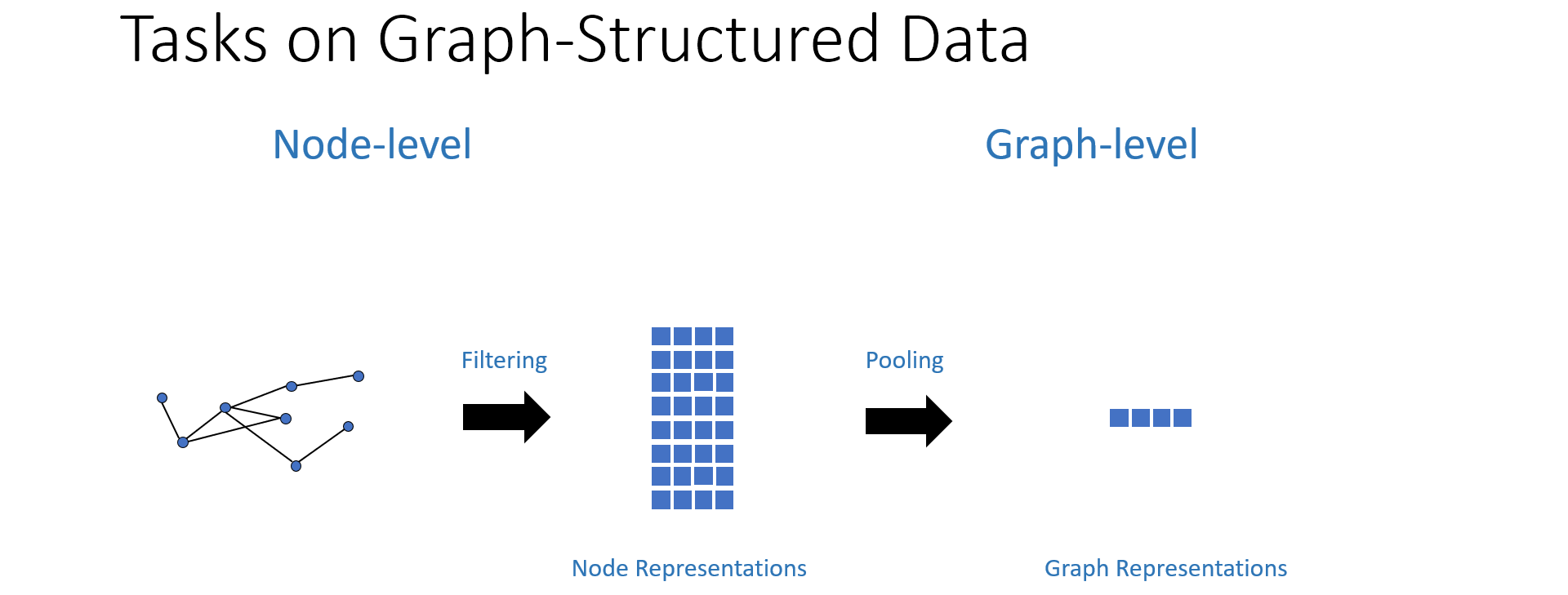
相应地,图神经网络模型中主要包含两类操作:
- 滤波(Filtering):取得节点表征(Node Representation),用于解决节点级任务;
- 池化(Pooling):降维取得图谱表征(Graph Representation),用于解决图谱级任务。
当然,在神经网络中还需要包含必要的激活(Activation)操作。
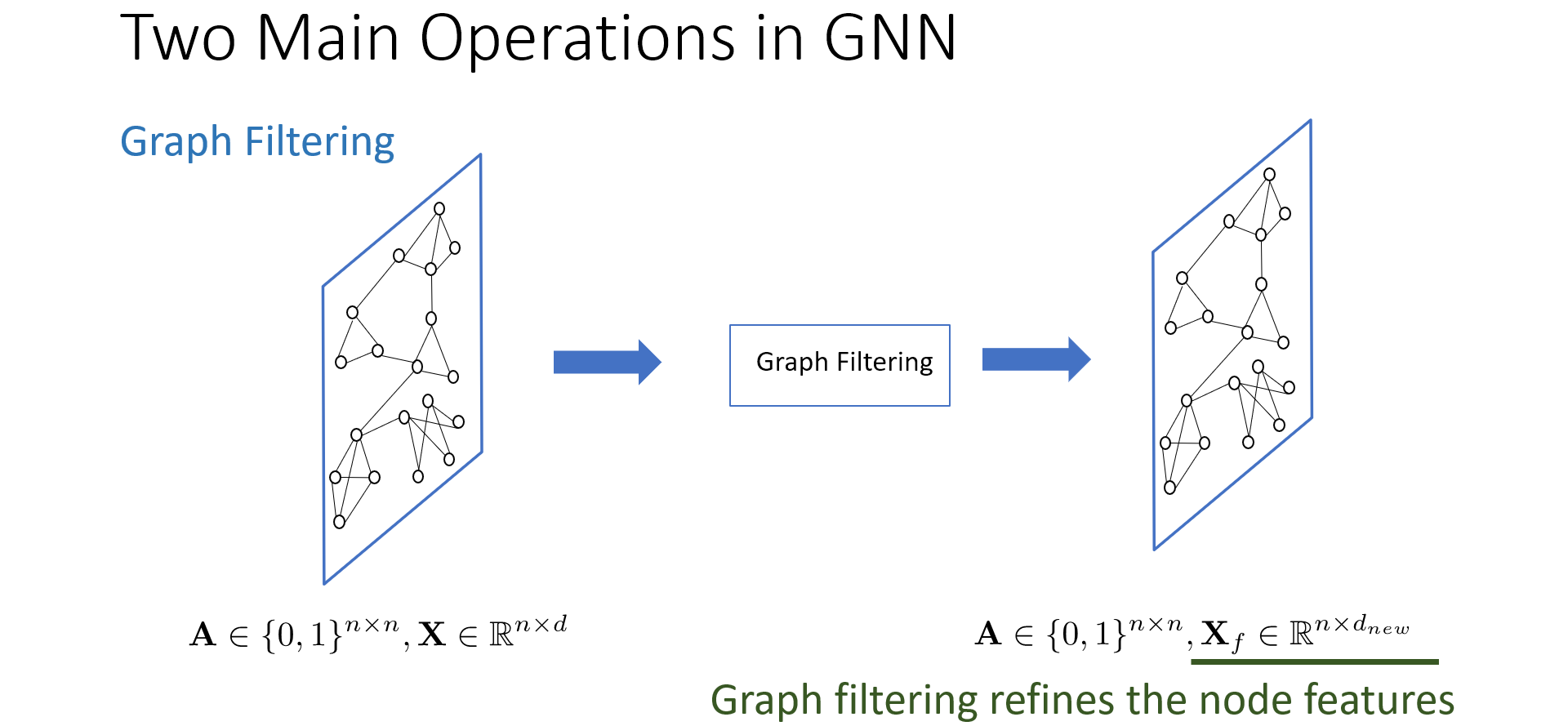
图滤波操作不改变图结构和节点数量,而是对图节点的特征向量进行变换,起到优化节点特征的作用。
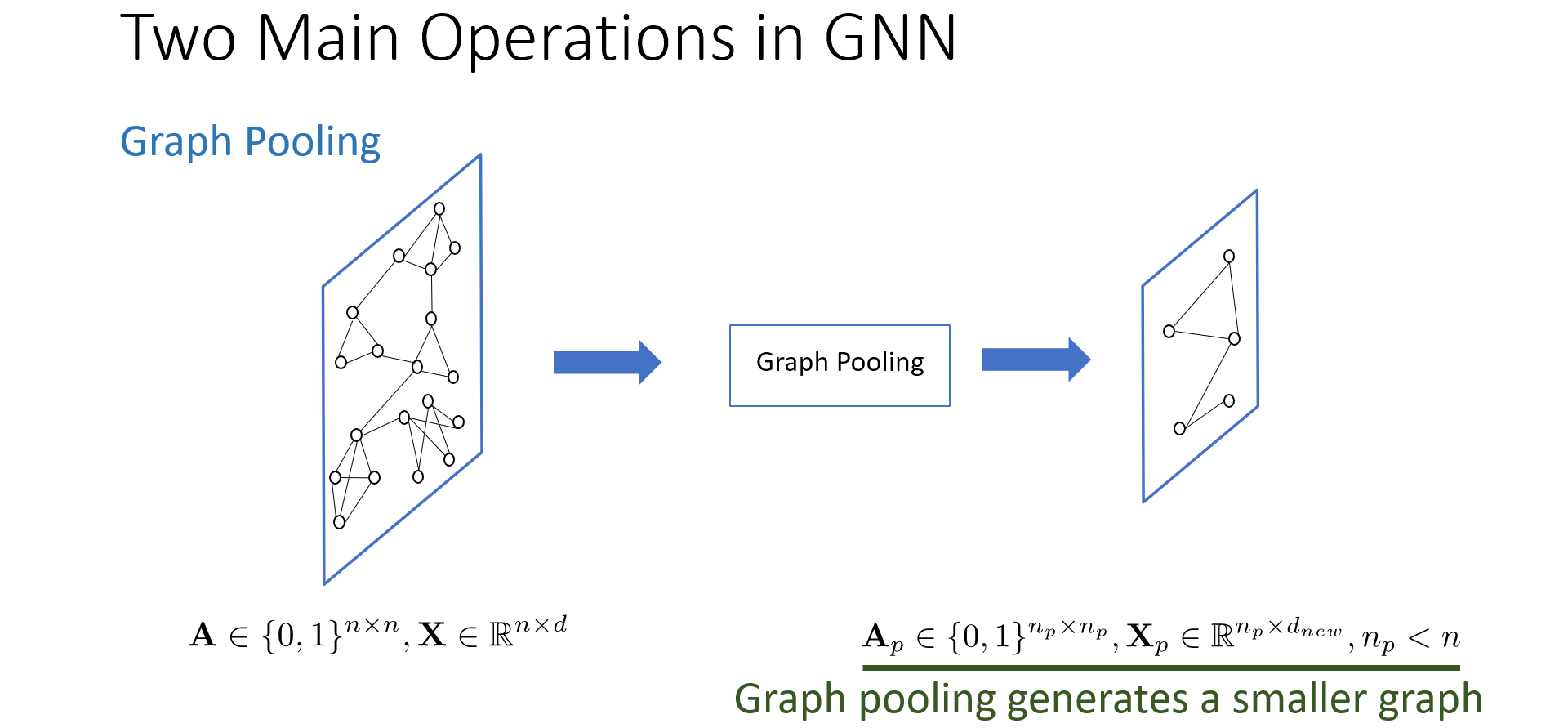
图池化操作会改变图结构和节点数量,池化操作减少了图中的节点数量,生成了一个更小的图,通常也伴随着特征向量的变换。
3.2 GNN中的滤波
图神经网络模型的研究主要关注于图神经网络中的滤波操作。
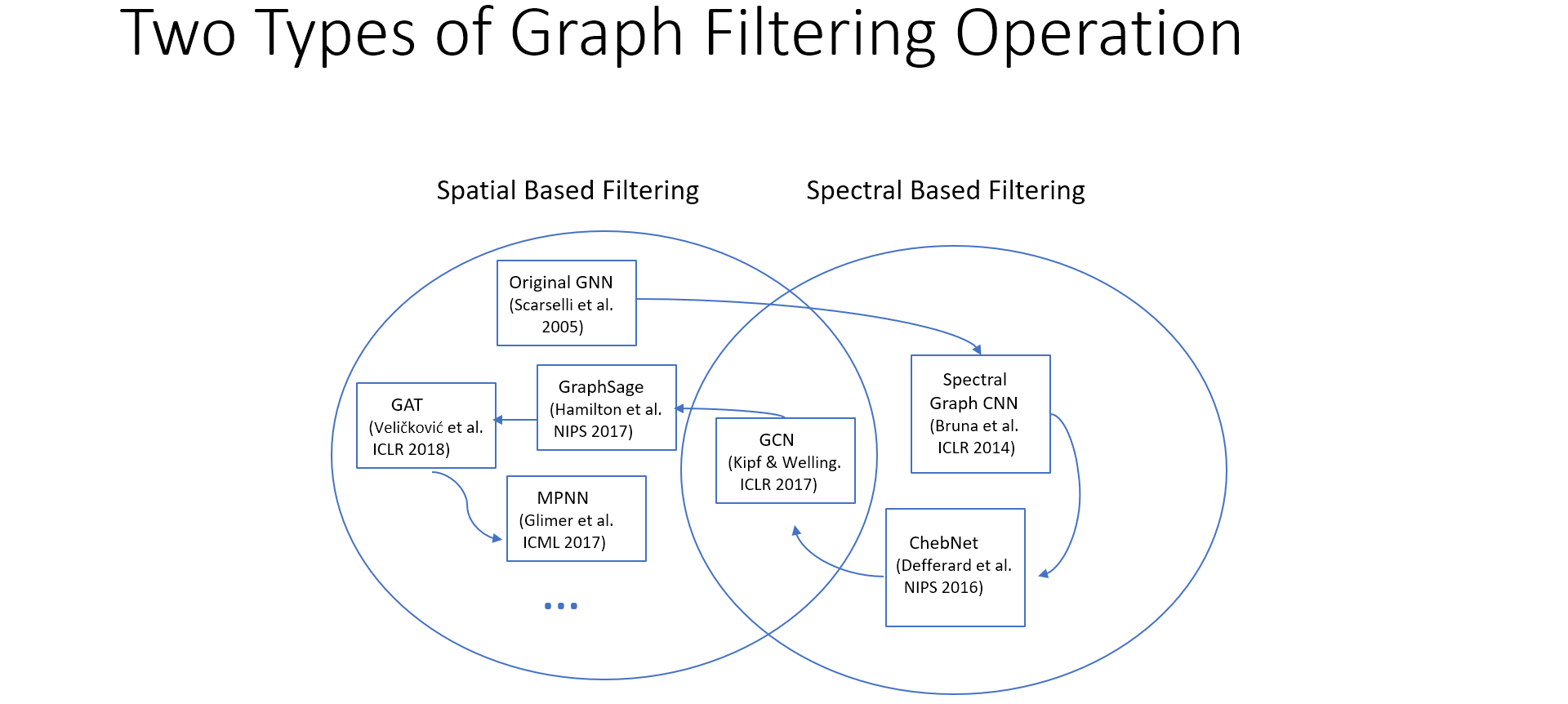
图卷积操作主要分为两类:
- 频域GNN(Spectral-based GNN)
- 空域GNN(Spatial-based GNN)
3.2.1 频域滤波
首先,理解矩阵特征值与特征向量。
从Interactive Linear Algebra一书中,给出了清晰的可视化解释,
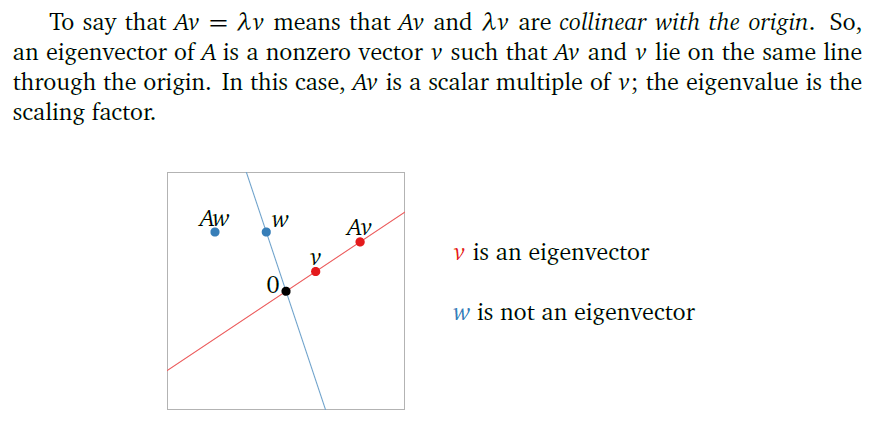
不难看出,\(Av=\lambda v\)体现的意义是,\(Av\)是和\(v\)的同方向向量,长度是\(v\)的\(\lambda\)倍。因此,特征向量\(v\)是\(A\)空间中的一个方向分量,而\(\lambda\)则体现了该方向向量\(v\)的在变换矩阵\(A\)中的重要性、权重。
具体地,在GNN频域滤波的语境中,基于谱图理论中拉普拉斯二次型的计算,特征值\(\lambda_i\)被解释为相应特征向量\(v_i\)的“频率”(frequency)。
因为拉普拉斯矩阵既可以表示图(graph)的特征(包含节点的度和邻接关系),又是实对称矩阵能够具备良好的特征分解性质,因此把图通过拉普拉斯矩阵进行表示。在拉普拉斯矩阵的特征分解\(L=U\Lambda U^T\)中,取得了特征向量组成的正交基\(U=[u_1, u_2, ... u_N] \in \mathbb{R}^{N \times N}\)和特征值组成的对角矩阵\(\Lambda = diag(\lambda_1, \lambda_2, ... \lambda_N)\)。
其中,对应特征值小,即“不重要”/“权重低”的特征向量被解释为“低频分量”,该特征向量表示的信号分量与整体信号相关性小,因此相邻节点之间,该信号分量波动不大,比较平滑,记录的是图中笼统的信息(信号整体的高低);而对应特征值大,即“重要”/“权重高”的特征向量被解释为“高频分量”,该特征向量表示的信号分量与信号波动的相关性高,因此相邻节点之间,该信号分量波动大,相对也就不平滑,记录的是图中细节的信息(节点之间的信号波动差异)。
所谓频域滤波,就是根据频率决定是保留还是滤除该分量。例如:高通滤波(high-pass)就是滤除低频分量,通过高频分量;低通滤波(low-pass)就是滤除高频分量,通过低频分量。
具体地,在GNN的频域滤波语境中,滤波器就可以形式化为: \[ \hat{g}(\lambda_i) \in \mathbb{R} \] 表示输入代表频率的特征值\(\lambda_i\),根据该输入,输出滤波后的权重。
例如,高通滤波就可以通过以下示例来表述: \[ \hat{g}(\lambda) = \begin{cases} 1& \lambda \ge threshold \\ 0& \lambda < threshold \end{cases} \] 整体来看,对正交基\(U\)中的特征向量\(u_i\),频域滤波的全过程形式化为: \[ f_i^{(filtered)} = u_i \hat{g}(\lambda_i) u_i^T f \] 对所有信号\(f \in \mathbb{R}^N\),频域滤波的矩阵形式化为: \[ \begin{equation} \begin{split} f^{(filtered)} & = U \hat{g}(\Lambda) U^T f \\ & = \begin{bmatrix} u_0 & ... & u_{N-1} \end{bmatrix} \begin{bmatrix} \hat{g}(\lambda_0) & & 0 \\ & \ddots \\ 0 & & \hat{g}(\lambda_{N-1}) \\ \end{bmatrix} \begin{bmatrix} u_0^T \\ \vdots \\ u_{N-1}^T \end{bmatrix} f \\ & = \begin{bmatrix} u_0 & ... & u_{N-1} \end{bmatrix} \begin{bmatrix} \hat{g}(\lambda_0) & & 0 \\ & \ddots \\ 0 & & \hat{g}(\lambda_{N-1}) \\ \end{bmatrix} \begin{bmatrix} \hat{f_0} \\ \vdots \\ \hat{f}_{N-1} \end{bmatrix} \\ & = \begin{bmatrix} u_0 & ... & u_{N-1} \end{bmatrix} \begin{bmatrix} \hat{g}(\lambda_0) \hat{f_0} \\ \vdots \\ \hat{g}(\lambda_{N-1}) \hat{f}_{N-1} \\ \end{bmatrix} \\ & = u_0 \hat{g}(\lambda_0) \hat{f_0} + ... + u_{N-1} \hat{g}(\lambda_{N-1}) \hat{f}_{N-1} \\ & = \sum_{i=0}^{N-1}u_i \hat{g}(\lambda_i) \hat{f_i} \end{split} \end{equation} \] 输出的滤波后的信号为\(f^{(filtered)} \in \mathbb{R}^N\)。
根据矩阵乘法的计算顺序,从右往左依次为:
- 傅里叶变换:对信号 \(f\) 进行傅里叶变换,取得相应于傅里叶模式 \(u_i\) 的傅里叶系数 \(\hat{f_i} = u_i^T f\) (或 \(\hat{f} = U^T f\) );
- 滤波:傅里叶变换得到了傅里叶模式 \(u_i\) 的傅里叶系数 \(\hat{f_i}\) ,那该傅里叶模式(即特征向量)是不是我们想要保留的呢?通过滤波,就可以根据该傅里叶模式(即特征向量)对应的频率(即特征值)进行滤波 \(\hat{g}(\lambda_i) u_i^T f\)(或\(\hat{g}(\Lambda) U^T f\));
- 逆傅里叶变换:将滤波过的傅里叶系数 \(\hat{g}(\lambda_i) \hat{f_i}\) 乘以对应的傅里叶分量(特征向量)\(u_i\),逆傅里叶变换为滤波过的空域信号\(f_i^{(filtered)}\)(或\(f^{(filtered)}\))。
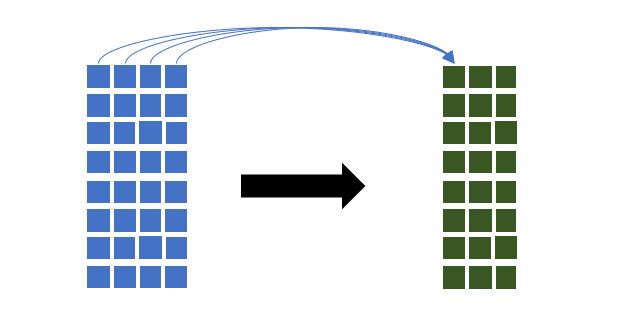
推广:推广到多通道信号的情况,每个节点信号均为\(d_1\)维向量(通道)的\(N\)个节点的图谱,即输入的空域图谱信号\(f \in \mathbb{R}^{N \times d_1}\),频域滤波类似地可形式化为: \[ f^{(filtered)} = U \begin{bmatrix} \sum_{i=1}^{d_1} \hat{g_{i,1}}(\Lambda) U^T f_{:,i} & \dots & \sum_{i=1}^{d_1} \hat{g_{i,d_2}}(\Lambda) U^T f_{:,{i}} \end{bmatrix} \] 输出的滤波后的信号为\(f^{(filtered)} \in \mathbb{R}^{N \times d_2}\)。也就是说,频域滤波不仅对信号进行了滤波,还可以调整输出的每个节点的信号维度(\(\mathbb{R}^{N\times d_1} \to \mathbb{R}^{ N \times d_2}\))。
分析滤波器参数规模:不难发现,从一个通道到另一个通道的频域滤波(即上图的一个箭头)对应一个滤波器。那么,从\(d_1\)个通道到\(d_2\)个通道的滤波变换,就需要有\(d_1 \times d_2\)个滤波器\(\hat{g}(\Lambda)\),每个滤波器为对角阵,包含\(N\)个参数。因此,该频域滤波的滤波器参数规模为\(d_1 \times d_2 \times N\)。
3.2.2 空域滤波
空域滤波的概念比较符合人的直觉,就是以节点在空域中的邻接节点作为其邻域,对该邻域做加权求和(卷积)即可。基于邻域的空域滤波可形式化为: \[ f_j^{(filtered)} = \sum_{i=0}^{N-1} F_{i,j} f_i \] 遍历节点\(j\)的邻域,对领域中的的每一个节点\(i\),都通过空域滤波器\(F \in \mathbb{R}^{N \times N}\)来对节点\(i\)的信号进行滤波。通过对邻域内的所有节点信号进行滤波加权平均,取得节点\(j\)的空域滤波结果。
对滤波结果,往往通过激活函数进行非线性变换,以及通过池化进行进一步处理,形式化为: \[ f_j^{pooled} = pooling(activation(f_j^{(filtered)})) \]
3.2.3 具体模型
3.2.3.1 GNN
【空域滤波】
Scarselli F, Tsoi A C, Gori M, et al. Graphical-based learning environments for pattern recognition[C]//Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR). Springer, Berlin, Heidelberg, 2004: 42-56.
图神经网络的概念最早由Franco Scarselli等人于2004年提出。
Scarselli等人在后续的论文中又反复研究了图神经网络的理论及应用。
Scarselli F, Yong S L, Gori M, et al. Graph neural networks for ranking web pages[C]//The 2005 IEEE/WIC/ACM International Conference on Web Intelligence (WI'05). IEEE, 2005: 666-672.
Scarselli F, Gori M, Tsoi A C, et al. The graph neural network model[J]. IEEE Transactions on Neural Networks, 2008, 20(1): 61-80.
首次提出的GNN将graph映射到一个实数向量,具体分两种: 1. graph-focused: 关注图结构,而无视涉及到的节点属性; 2. node-focused: 根据节点属性将图映射到向量。
最早的GNN的核心思想是,用一个实数向量\(x_n\)来表示节点\(n\)的状态(state)。
该状态向量\(x_n\)取决于其领域中的信息,包含: 1. \(n\)的标签; 2. \(n\)的连接边的标签; 3. \(n\)的邻居节点的状态向量和标签。
具体计算公式为: \[ x_n = \sum_{u\in ne[n]} h_w(l_n, x_u, l_u), n\in N. \] 在该式中,节点\(n\)的状态取决于: 1. \(l_n\),节点\(n\)的标签(Label); 2. \(x_u\),邻居节点\(u\)的状态; 3. \(l_u\),邻居节点\(u\)的标签。
显然,节点\(n\)的状态是通过对节点自身以及邻域节点的信息进行滤波取得的,属于空域滤波。
3.2.3.2 Spectral Graph CNN
【频域滤波】
Bruna J, Zaremba W, Szlam A, et al. Spectral networks and locally connected networks on graphs[J]. arXiv preprint arXiv:1312.6203, 2013.
这篇论文主要研究如何把CNN用到图谱的处理上去。可以理解为这是第一代的GCN。
可以说是GCN的早期研究。论文给出了两种滤波方式,分别对应空域滤波和频域滤波。
论文写的在我看来写得比较晦涩,而且公式琢磨着总感觉有小错误,原理可以参考上述3.2.1和3.2.2分别介绍的频域滤波和空域滤波,是一致的。
在这篇论文中,滤波器就是简单地套上了拉普拉斯矩阵的特征值(加了层非线性变换激活函数),作为初代设计,比较简单粗暴,仅仅使用参数\(\theta\)来近似滤波器函数: \[ \hat{g}(\Lambda) = diag(\hat{g}(\lambda_0), ..., \hat{g}(\lambda_{N-1})) = diag(\theta_0, ..., \theta_{N-1}) \] 展开表示,就是: \[ \hat{g}(\Lambda) = \begin{bmatrix} \hat{g}(\lambda_0) & & 0 \\ & \ddots & \\ 0 & & \hat{g}(\lambda_{N-1})\\ \end{bmatrix} = \begin{bmatrix} \theta_0 & & 0 \\ & \ddots & \\ 0 & & \theta_{N-1} \\ \end{bmatrix} \] 此处的\(\theta \in \mathbb{R}^{N}\)是模型的可学习参数。
这种滤波器设计相当于是为每一个节点都计算一个频域滤波值。
不难看出,每个滤波器(卷积核)包含\(N\)个参数\(\theta \in \mathbb{R}^N\),这个\(N\)取决于数据规模,一旦节点规模很大,滤波器的参数量就会跟着很大。如果要实现输入\(f_{in} \in \mathbb{R}^{N \times d_1}\)到\(f_{out} \in \mathbb{R}^{N \times d_2}\)的频域滤波,就需要\(d_1 \times d_2 \times N\)的滤波器参数规模。
缺陷:
1.滤波函数近似效果差;
2.滤波器完全依赖于训练时的图谱,无法迁移变通,每一个滤波值都是和对应节点绑定的;
3.模型参数规模庞大,因为一个图谱的节点数量\(N\)往往是很大的。
3.2.3.3 ChebNet
【频域滤波】
Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//Advances in neural information processing systems. 2016: 3844-3852.
这篇论文主要研究在把CNN用到图谱的频域滤波的基础之上,如何改进滤波器的设计。可以理解为这是第二代的GCN。
ChebNet中,首先定义使用的拉普拉斯矩阵不再是基本的\(L=D-A\),而是规格化(normalized)拉普拉斯矩阵,即:\(L = I_N - D^{-1/2} A D^{-1/2}\)。
使用多项式函数近似滤波器函数
所谓多项式(\(K\)阶),就是: \[ p_k(x) = \sum_{k=0}^K \theta_k x^k = \theta_0 + \theta_1 x + \theta_2 x^2 + \dots + \theta_K x^K \] 通过多项式来近似滤波器,作为滤波器,形式化表示为: \[ \hat{g}(\Lambda) = \sum_{k=0}^{K-1} \theta_k \Lambda^k = \begin{bmatrix} \sum_{k=0}^{K-1} \theta_k \lambda_0^k & & 0 \\ & \ddots & \\ 0 & & \sum_{k=0}^{K-1} \theta_k \lambda_{N-1}^k\\ \end{bmatrix} \] 由于通过多项式函数来近似滤波器,参数就只有\(K\)个,即\([\theta_0, ... , \theta_{K-1}]\),在模型训练过程中被优化。这意味着卷积核(滤波器)的参数规模不再受数据规模\(N\)影响。每个滤波器\(K\)个参数,意味着从\(d_1\)个通道到\(d_2\)个通道的滤波映射,需要\(d_1 \times d_2 \times K\)的参数规模。在实践中,相较于\(d_1 \times d_2 \times N\)是大大减小了。而且,滤波器参数与节点数量\(N\)脱钩,还使得训练出的滤波器,使用上不再仅限于当前图谱,而是可适应图谱节点数量、图谱结构的变化。
而且巧的是,使用这个滤波器来滤波傅里叶变换的频域信号,特征值矩阵和特征向量矩阵相乘,刚好就还原了拉普拉斯矩阵(\(U \Lambda^k U^T = L^k\)),也就是说——不需要再计算拉普拉斯矩阵特征分解了,一下子减少了计算代价。频域滤波过程推导如下: \[ U \hat{g}(\Lambda) U^T f = U \sum_{k=0}^{K-1} \theta_k \Lambda^k U^T f = \sum_{k=0}^{K-1} \theta_k L^k f \] 解释一下,因为\(U\)是正交阵,满足\(U^T = U^{-1}\),所以此处涉及的数学原理是: \[ U \Lambda^k U^T = (U \Lambda U^T)(U \Lambda U^T)\dots(U \Lambda U^T) = L^k \] 可见,对于多项式形式的滤波器,拉普拉斯矩阵的特征分解刚好被还原了,所以只需要计算拉普拉斯矩阵的幂就可以了。
另外,拉普拉斯矩阵\(L\)体现的是图节点之间的直接的邻接关系,而\(L^K\)则体现了图节点之间的\(K\)跳内的连通关系。因此,\(\sum_{k=0}^{K-1} \theta_k L^k\)意味着计入了从1跳到K跳的节点间联通关系。这使得多项式参数滤波器能够准确地将滤波作用定位于半径为\(K\)跳的邻域范围内。
使用切比雪夫多项式近似滤波器函数
以上解释了多项式滤波器相较于简单的参数滤波器的好处,ChebNet则是把一般多项式\(p_K(x) = \sum_{k=0}^{K-1}\theta_k x^k\)替换为了切比雪夫多项式\(T_K(x) = \sum_{k=0}^{K-1} \theta_k T_k(x)\)。
在输入参数上,ChebNet对切比雪夫多项式\(T_k(x)\)的输入参数\(x\)进行了缩放(scale)处理。因为当\(x \in [-1,1]\)时,切比雪夫多项式\(T_k(x)\)满足三角函数表达式\(T_k(x) = \cos(k \arccos(x))\)。这个数学性质使得切比雪夫多项式的值域能够稳定在上界为1,下界为-1的区间内,即使得\(T_k(x) \in [-1,1]\)。
数学参阅:2011 Wavelets on graphs via spectral graph theory
具体地,在ChebNet中,切比雪夫多项式的输入参数\(\tilde{\Lambda}\)是一个缩放对角阵: \[ \tilde{\Lambda} = \frac{2 \Lambda}{\lambda_{max}} - I_N \] 该\(\tilde{\Lambda}\)是对拉普拉斯特征值对角阵\(\Lambda\)进行缩放的结果,将特征值从\([0,\lambda_{max}]\)缩放至\([-1,1]\)以满足上述性质。
这样一来,滤波器\(\hat{g}(\Lambda)\)被修改为\(\hat{g}(\tilde{\Lambda})\): \[ \hat{g}(\tilde{\Lambda}) = \sum_{k=0}^{K-1} \theta_k T_k(\tilde{\Lambda}) = \begin{bmatrix} \sum_{k=0}^{K-1} \theta_k T_k(\tilde{\lambda}_0) & & 0 \\ & \ddots & \\ 0 & & \sum_{k=0}^{K-1} \theta_k T_k(\tilde{\lambda}_{N-1}) \\ \end{bmatrix} \]
其中,\(k\)阶切比雪夫多项式\(T_k(x)\)定义为: \[ T_k(x) = 2xT_{k-1}(x) - T_{k-2}(x) \] 切比雪夫多项式是递归定义的多项式,它的初始项\(T_0 = 1\),\(T_1 = x\)。
同样地,切比雪夫多项式虽然是递归定义的,但代入展开后也是一种多项式,也满足一般多项式所具备的省去矩阵特征分解的计算代价、K跳局部性的特性。
将该滤波器代入频域滤波函数,可推得: \[ f^{(filtered)} = U \hat{g}(\tilde{\Lambda}) U^T f = U \sum_{k=0}^{K-1}\theta_k T_k(\tilde{\Lambda}) U^T f = \sum_{k=0}^{K-1}\theta_k T_k(\tilde{L}) f = \hat{g}(\tilde{L}) f \] 其中,\(\tilde{L}\)是对拉普拉斯矩阵的缩放结果: \[ \tilde{L} = \frac{2 L}{\lambda_{max}} - I_N \]
延伸问题:为什么要用切比雪夫多项式呢?
以下示例参阅:
Hammond D K, Vandergheynst P, Gribonval R. Wavelets on graphs via spectral graph theory[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 129-150.
数学理论由来参阅:
Geddes K O. Near-minimax polynomial approximation in an elliptical region[J]. SIAM Journal on Numerical Analysis, 1978, 15(6): 1225-1233.
涉及到数学层面的分析,大概的感性理解是,一般多项式在系数变化时,扰动大,而切比雪夫多项式更加抗扰动。尤其是目标函数变化比较平缓时,切比雪夫多项式要平缓的多,近似误差小得多。
对\(f(x)\)目标函数的\(n+2\)个采样点\([x_1, x_2, \dots, x_{n+2}]\)进行近似时,极小极大近似算法(minimax approximation algorithm),典型代表如:Remez algorithm(Remez exchange algorithm)可以使得\(n\)阶多项式\(P_n(x)=a_0 + a_1 x + a_2 x^2 + \dots + a_n x^n\)对目标函数实现minimax近似(最小化最大误差,使\(n+2\)个采样点的最大误差最小化),形式化为,解线性方程系统: \[ a_0 + a_1 x_i + a_2 x_i^2 + \dots + a_n x_i^n + (-1)^i E = f(x)\qquad(where\quad i=1,2,\dots,n+2) \] 其中\[a_0, a_1, \dots, a_n\]是多项式\[P_n(x)\]的多项式系数。
如图:
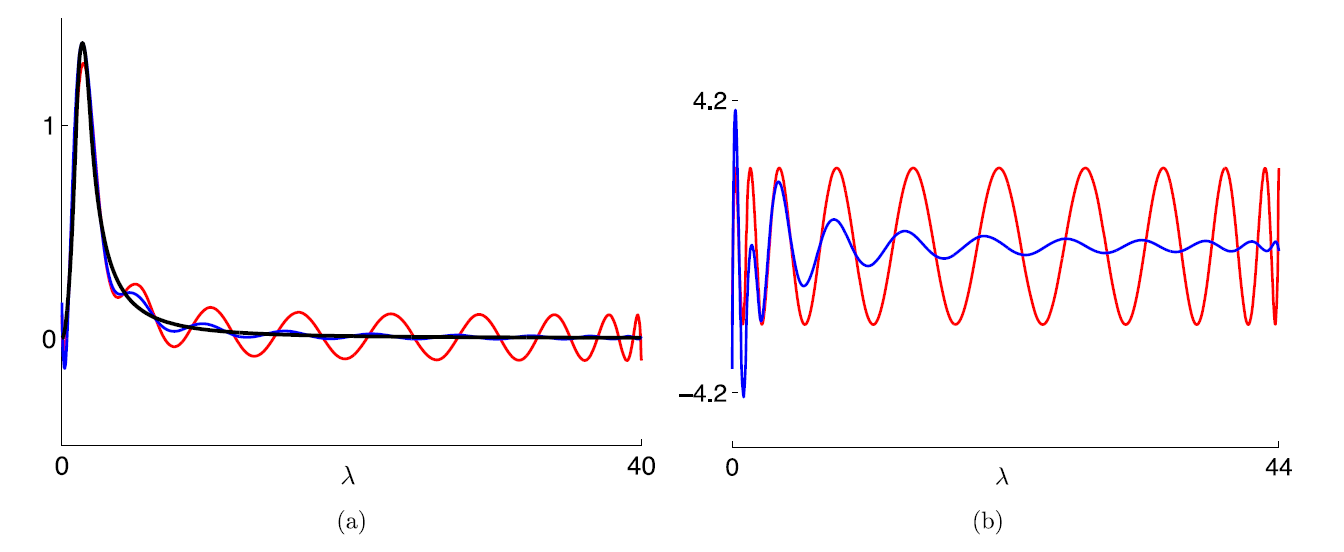
- 左图(a)中,黑色表示目标函数,为小波核函数\(g(\lambda)\),蓝色表示截断切比雪夫展开式(truncated Chebyshev expansion),红色表示minimax多项式近似。
- 右图(b)中,表示的是两个近似函数,即截断切比雪夫展开式和minimax多项式,与目标函数的近似误差。
左图(a)中,近似函数与目标函数看起来“相交”的地方,就是采样点位置,经过近似计算,这些采样点的位置的近似误差很小。而采样点之外的地方,近似函数和目标函数可能高度拟合,也可能出现大幅震荡(参考数值计算中的“龙格现象(Runge phenomenon)”)。
进一步查看右图(b)不难发现,以2011年这篇论文研究的小波核为例,截断切比雪夫展开式(蓝色)的最大误差只比真正的minimax多项式(红色)略大一点。但是,在目标函数变化比较平滑的部分,截断切比雪夫展开式的近似误差比minimax多项式的近似误差要低得多。因为其近似出的多项式函数更加平滑,不像minimax多项式那样频繁大幅震荡。
3.2.3.4 GCN
【频域滤波】
Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.
Graph Convolutional Network (GCN)
本文提出图卷积网络,实际上并不算是第一个图谱上的卷积网络。上述的Spectral Graph CNN和ChebNet等工作都是图卷积网络的研究工作。
本文的GCN主要是对ChebNet进行了一系列简化和改进。
简化改进的目的,是为了建立深层的神经网络,即,简化每一层的计算复杂度,从而让深层的图卷积成为可能。
如上文所述,ChebNet通过切比雪夫多项式来近似滤波器函数\(\hat{g}(\Lambda)\),已经推得了: \[ f^{(filtered)} = U^T \hat{g}(\tilde{\Lambda}) U f = U^T \sum_{k=0}^{K}\theta_k T_k(\tilde{\Lambda}) U f = \sum_{k=0}^{K}\theta_k T_k(\tilde{L}) f = \hat{g}(\tilde{L}) f \] 其中,\(\tilde{\Lambda} = \frac{2 \Lambda}{\lambda_{max}} - I_N\),\(\tilde{L} = \frac{2 L}{\lambda_{max}} - I_N\)。
本文的GCN所作出的具体的改变为:
简化1:一阶切比雪夫多项式及系数约束
GCN将切比雪夫展开式限制为1阶,即\(K=1\),则滤波器函数表示为: \[ g(\lambda) = \sum_{k=0}^1 \theta_k T_k(\lambda) = \theta_0 T_0(\lambda) + \theta_1 T_1(\lambda) = \theta_0 + \theta_1 \lambda \] 对于一阶切比雪夫多项式,GCN还增加了限制条件,限定\(\theta = \theta_0 = - \theta_1\),使参数只剩\(\theta \in \mathbb{R}\)一项。滤波器函数表示为: \[ g(\lambda) = \theta - \theta \lambda = \theta(1 - \lambda) \] 简化2:特征值约束
GCN将特征值的最大值限定为2,即\(\lambda_{max} = 2\)。
这样的约束使得缩放拉普拉斯矩阵\(\tilde{L}\)进一步简化为: \[ \tilde{L} = L - I_N = (I_N - D^{-1/2} A D^{-1/2}) - I_N = - D^{-1/2} A D^{-1/2} \]
简化到这一步,基于以上限制条件,完整的滤波函数可推得: \[ f^{(filtered)} = \hat{g}(\tilde{L}) f = \theta (I_N - \tilde{L}) = \theta (I_N + D^{-1/2} A D^{-1/2}) f \] 简化3:重规格化技巧
作者提出了一项重规格化技巧(renormalization trick),使得滤波计算进一步简化。该技巧形式化为: \[ I_N + D^{-1/2} A D^{-1/2} \to \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} \] 其中,\(\tilde{A} = A + I_N\),度矩阵基于邻接矩阵计算,也改为\(\tilde{D}_{ii} = \sum_{j} \tilde{A}_{ij}\)。
经过该技巧的进一步简化,GCN每层的滤波函数就变为: \[ f^{(filtered)} = \hat{g}(\tilde{L}) f = \theta (I_N - \tilde{L}) = \theta (I_N + D^{-1/2} A D^{-1/2}) f = \theta (\tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2}) f \] 最终形式
GCN可以用于多通道的信号处理,对于从\(d_1\)个通道的输入信号到\(d_2\)个通道的输出信号的滤波映射,GCN的一层可形式化为以下矩阵形式: \[ Z = \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} X \Theta \]
其中:
- \(X \in \mathbb{R}^{N \times d_1}\)表示频域滤波前的输入信号;
- \(\Theta \in \mathbb{R}^{d_1 \times d_2}\)表示\(d_1 \times d_2\)个滤波的参数;
- \(Z \in \mathbb{R}^{N \times d_2}\)表示频域滤波后的输出信号。
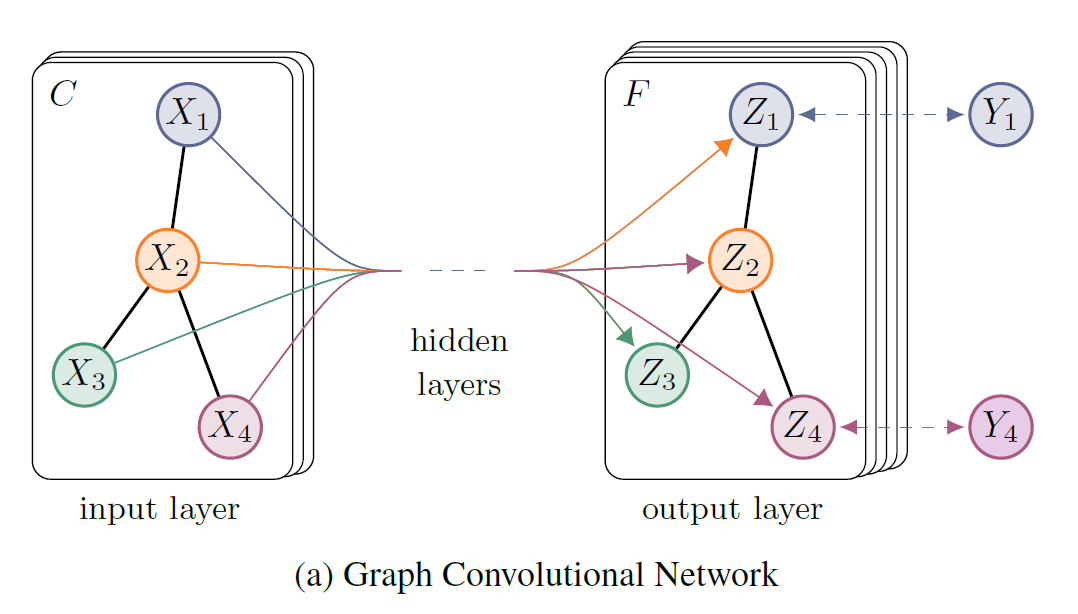
由此,就可以建立多层的GCN网络,以2层的GCN网络为例: \[ Z = f(X, A) = softmax(\hat{A}\; \mathrm{ReLU}(\hat{A} X W^{(0)})W^{(1)}) \] 其中,\(\hat{A} = \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2}\)。
GCN可以用于实现半监督学习,即,以有标签的节点来计算损失,进行训练。具体的,论文中基于有标签节点计算交叉熵损失: \[ \mathcal{L} = - \sum_{l \in \mathcal{Y}_L} \sum_{f=1}^F Y_{lf} \ln Z_{lf} \] 其中,\(\mathcal{Y}_L\)是有标签的节点序号集合。
实验评价

本文设计的GCN做出的简化到底有没有意义呢?从实验结果来看,简化整体上提升了实验效果。
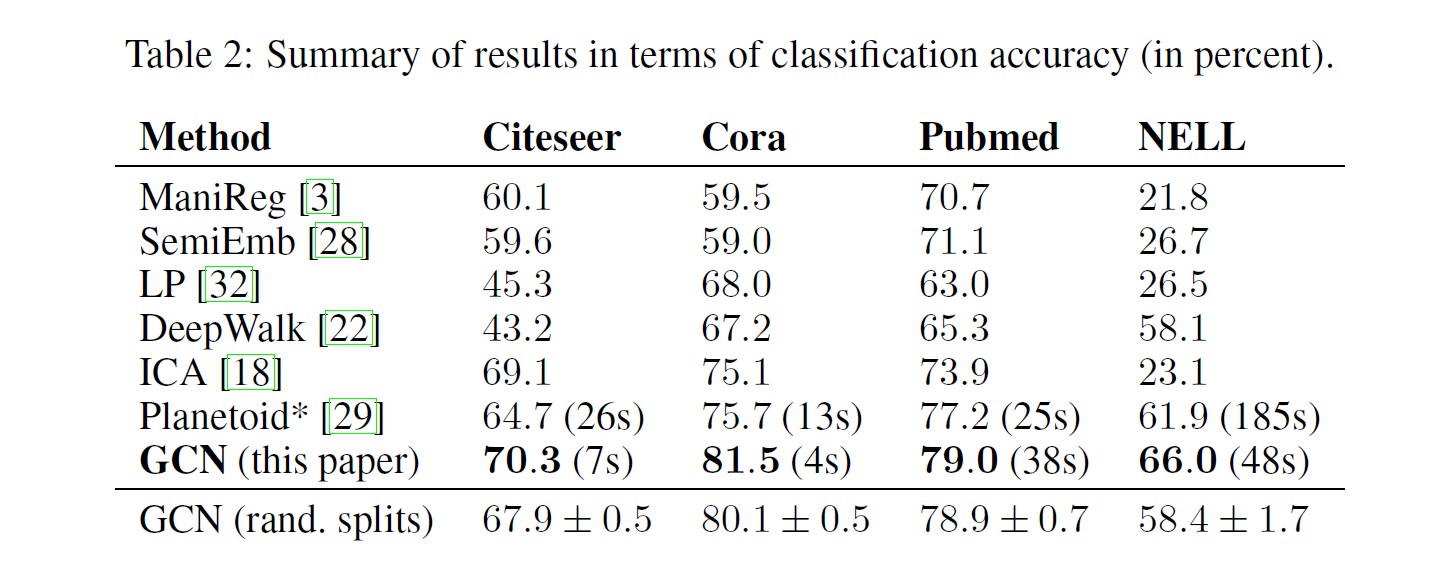
相比其他模型,GCN在几个数据集上的分类准确率结果均为领先,而且速度更快。
3.2.3.5 GraphSage
3.2.3.6 GAT
3.2.3.7 MPNN
3.3 GNN中的池化
3.3.1 gPool
3.3.2 DiffPool
3.3.3 Eigenpooling
3.4 GNN的鲁棒性
Robustness of GNN
3.5 GNN的扩展学习
Scalable Learning for GNN